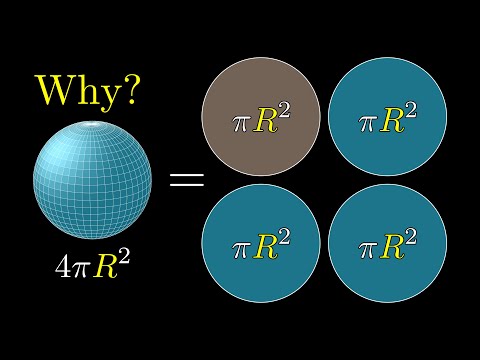For example, the space that a substance or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas.
Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. Is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.
Professional people always ensure, and their success in fine cooking depends on, they get the most precise units conversion results in measuring their ingredients. In speciality cooking an accurate volume and capacity unit measure can be totally crucial. The radius of a sphere is the distance from the exact center of the sphere to a point on the outside edge of that sphere. However, you can also work backward from the diameter, circumference, etc. to find the sphere's radius.
Use the formula that works with the information you have. A sphere is the shape of a basketball, like a three-dimensional circle. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference.
Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C. It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . Conversion for how many gallons liquid US, gal, of volume and capacity units, are contained in a one-foot diameter sphere, ∅ 1 ft?
Or, how much in gallons liquid US volume and capacity in 1 one-foot diameter sphere? To link to this volume and capacity - one-foot diameter sphere to gallons liquid US on line culinary converter for the answer, simply cut and paste the following. The volume of a cylinder is equal to the product of the area of the circular base and the height of the cylinder. The volume of a cylinder is measured in cubic units. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches. A sphere is a 3-dimensional round object.
The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. In this calculation you can calculate the volume of a sphere with a number of given input values, such as radius, diameter, circumference. You also have a number of different input units and can choose output unit according to your likings.
Culinary volume and capacity converter from ∅ 1 ft ( one-foot diameter spheres ) measure to gal equivalent. To calculate the volume of a cylinder, you need the radius or diameter of the circular base or top and a cylinder's height. Remember that a great circle will always cut a sphere into two equal hemispheres. Consequently, we can use information about great circles to help us calculate the surface area of corresponding hemispheres or other fractions of a sphere.
There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center.
The volume of a sphere is measured in cubic units. Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. The volume of a sphere formula can be found in terms of the diameter. The diameter of a sphere is the longest line that is inside the sphere and that passes through the center of the sphere. A sphere is a three-dimensional shape that is perfectly symmetrical and round in shape.
Some examples of spheres are a ball, a globe, etc. The volume of a sphere is the amount of space that is inside it the capacity of the sphere that it can hold. In this article, we will derive the diameter of a sphere formula using the volume.
This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's". The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious. So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind.
If you want to help here I think you should pay attention to new questions that don't yet have answers. Calculate gallons liquid US in volume and capacity per 1 one-foot diameter sphere unit. The volume and capacity kitchen measuring units converter for culinary chefs, bakers and other professionals. The baseball is not regulation size.
If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r. The radius is 3/2 inches, so I double that to find the diameter. The diameter of the ball is 3 inches, which is greater than the allowed range of diameters. So far we've calculated the volume of cubes, rectangular tanks, and cylinders. Using that information, how do you think we would calculate the volume of a sphere?
What variables do you think you would use? Take a few moments to think about it before we go through the explanation below. And to get the volume of a right circular cylinder, you take pi times the radius squared times the height. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button.
They can use these methods in order to determine the surface area and volume of parts of a sphere. The volume of a 3 -dimensional solid is the amount of space it occupies. Volume is measured in cubic units.
Be sure that all of the measurements are in the same unit before computing the volume. A glass dome for a lighting fixture is in the shape of a hemisphere. The circumference of the great circle of the hemisphere is 12π inches. Which statements about the hemisphere are true?
The total surface area is 108π square inches. The total surface area is 144π square inches. The total surface area is 432π square inches. The total surface area is 36π square inches. Simply enter the desired value in the relevant box. Please use only numbers (e.g. enter 22 not 22 cm).
This calculator only uses numbers. If you try to enter a unit of measure (e.g. 22 metres, 4 miles, 10 cm) you will get an NAN error appear in each box. When you have entered the number that you know, click the button on the right of that box to calculate all the other values. For example, if you know the volume of a sphere enter the value into the bottom box and then click the calculate button at bottom right.
In other words, to get the surface area of a sphere, you take four times pi times the radius squared. And to get the volume of a sphere, you take the 4/3 of pi times the radius cubed. A sphere is the 3- D shape where the curved surface area equals to the total surface area of the figure.
The curved surface area is the area in which only the area of the curved part is covered. The formula does not take into account the circular base. Street light post The post of a street light is shaped like a truncated cone, as shown in the picture below. It is a large cone minus a smaller top cone.
The large cone is 30 feet tall with base radius 1 foot. The smaller cone is 10 feet tall with base radius of 0.5 feet. To the nearest tenth, find the volume of the large cone. Find the volume of the small cone.
Find the volume of the post by subtracting the volume of the small cone from the volume of the large cone. How many cubic inches of candy will fit in a cone-shaped piñata that is 18 inches long and 12 inches across its base? Round the answer to the nearest hundredth. In geometry, a cone is a solid figure with one circular base and a vertex.
Find the volume and surface area of a can of paint with radius 8 centimeters and height 19 centimeters. Assume the can is shaped exactly like a cylinder. Find the volume and surface area of a can of soda. The radius of the base is 4 centimeters and the height is 13 centimeters.
A globe of Earth is in the shape of a sphere with radius 14 centimeters. A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.
A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter.
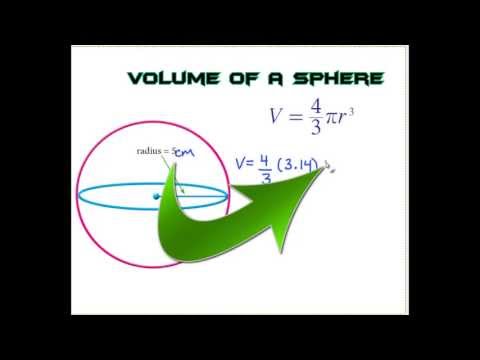
Two spheres of the same radius are congruent. A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters. The formula for the volume of a sphere is 4/3 times pi times the radius cubed.
Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. The volume of a hemisphere is equal to two-thirds of the product of pi and the cube of the radius. Is a solid figure with one circular base and a vertex.
Surface area of a can of paint with radius 8 centimeters and height 19 centimeters. Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 44 by 22 by 33 rectangular solid has 2424 cubic units. However, using calculus, the volume of a cone is the integral of an infinite number of infinitesimally thin circular disks of thickness dx.
The calculation for the volume of a cone of height h, whose base is centered at with radius r, is as follows. Well I wasn't really going for elementary, just a dumbed down version that worked for me that might help others starting at University Math. The other answers were great with backgrounds of why a sphere fits into a cylinder, etc, so I left that part out of mine. I personally wasn't able to figure out where 4/3 came from using any of their answers, so I contributed mine to help those that may see things my way. I agree it is an old question, but I had this question in 2019 that I couldn't find the answer to with those answers.